class: center, middle, inverse, title-slide # MCO: inferencia y levantamiento de supuestos ## Econometría I ### Paula Pereda (<a href="mailto:ppereda@correo.um.edu.uy" class="email">ppereda@correo.um.edu.uy</a>) ### 17 de setiembre de 2021 --- class: inverse, middle # Bondad de ajuste --- layout: true # Bondad de ajuste --- ## Estadístico t - ¡de nuevo! El modelo poblacional lo escribimos de la siguiente manera: `$$y=\beta_{0}+\beta_{1} x_{1}+\ldots+\beta_{k} x_{k}+\mu$$` .hi-purple[Distribución t para estimadores estandarizados:] Bajo los supuestos del modelo lineal clásico (MLC), `$$\left(\hat{\beta}_{j}-\beta_{j}\right) / \operatorname{ee}\left(\hat{\beta}_{j}\right) \sim t_{n-k-1}$$` donde `\(k+1\)` es la cantidad de parámetros desconocidos en el modelo poblacional `\(y=\beta_{0}+\beta_{1} x_{1}+\ldots+\beta_{k} x_{k}+\mu\)`, o sea `\(k\)` parámetros de pendiente y el intercepto `\(\beta_{0}\)`. - Testeo: `\(\left.H_{0} \ \right) \beta_{j}=0\)` - Ejemplo: `\(\text{salario}_i = \beta_0 + \beta_1 \, \text{educación}_i + \beta_2 \, \text{experiencia}_i + \beta_3 \, \text{antigüedad}_i + \mu_i\)` - ¿Qué significa testear: `\(\left.H_{0} \ \right) \beta_{j}=0\)` en este caso? 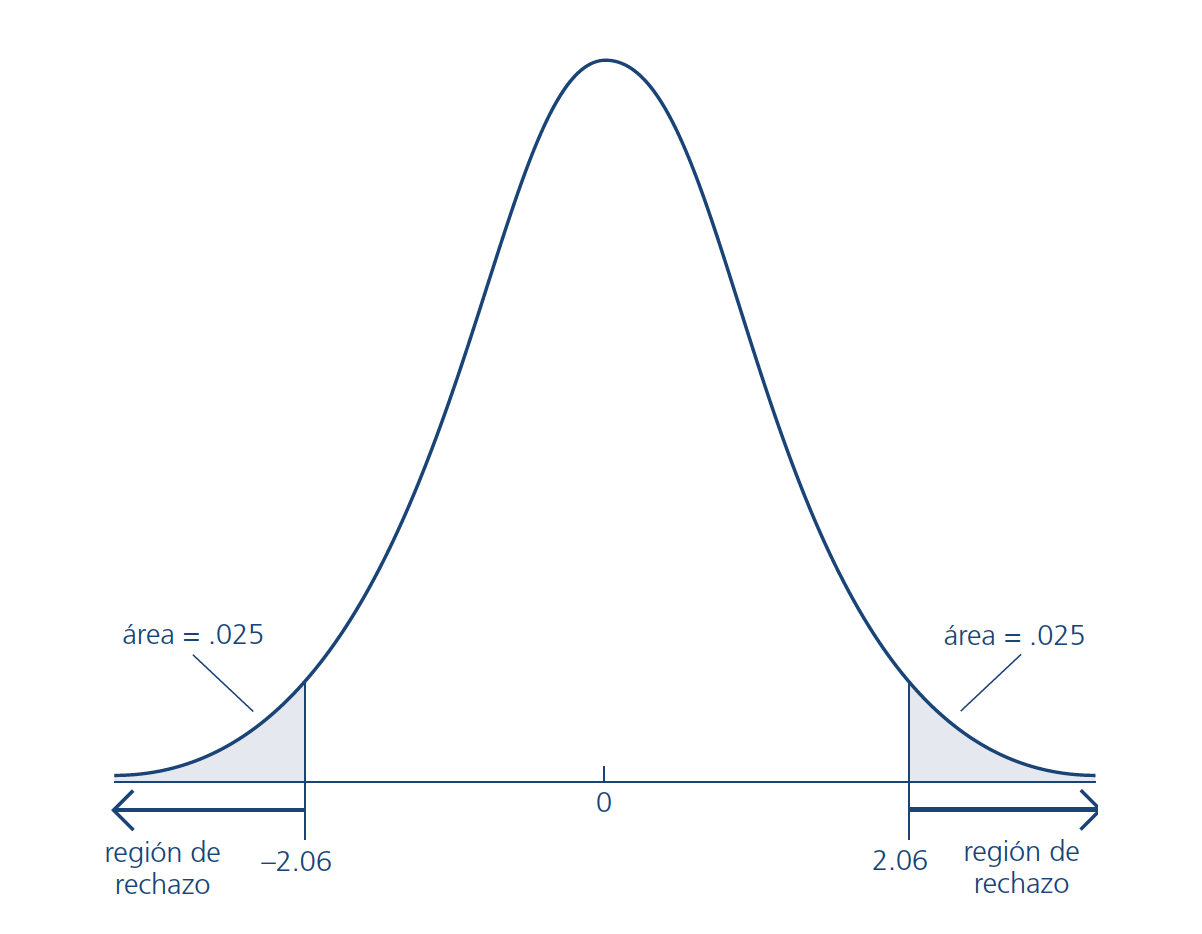--- ## Estadístico de prueba `\(t\)` `$$t_{\hat{\beta}_{j}}=\frac{\hat{\beta}_{j}}{\operatorname{ee}\left(\hat{\beta}_{j}\right)}$$` .pull-left[ - A dos colas la regla de rechazo es `\(\left|t_{\hat{\beta}_{j}}\right|>c\)` - Para encontrar `\(c\)`, definir `\(\alpha\)`, en general 5% - Suponiendo que `\(N-k-1 = 25\)`] .pull-right[ <img src="images/region_rechazo.png" width="500">] --- ## Valor-p para el estadístico `\(t\)` Alternativamente, podemos calcular el ** valor p ** que acompaña a nuestro estadístico de prueba, que efectivamente nos da la probabilidad de ver nuestro estadístico de prueba *o nuestro estadístico de prueba más extrema* si la hipótesis nula fuera cierta. Valores `\(p\)` muy pequeños, generalmente `\(<0.05\)`, significan que sería poco probable que veamos nuestros resultados si la hipótesis nula fuera realmente cierta; tendemos a rechazar el valor nulo para valores `\(p\)` por debajo de `\(0.05\)`. --- ## Valor-p para el estadístico `\(t\)` - Quitar arbitriariedad del nivel de significación elegido  - El valor `\(p\)` es la probabilidad de obtener valores de la prueba estadística que sean mayores o iguales (o más extremos) que el efectivamente observado si `\(\left.H_{0} \ \right)\)` es cierto - No rechazar `\(\left.H_{0} \ \right)\)` si `\(p > \alpha\)`. En otro caso rechazar. Cuanto más chico es el `\(p\)` más fuerte es el rechazo. - Recordar que, en principio, queremos rechazar `\(\left.H_{0} \ \right)\)` pues esto implica decir que hay evidencia para decir que `\(\beta_j\)` es significativamente diferente de cero. --- ## Estadístico F - El estadístico F se utiliza para contrastar hipótesis conjuntas sobre los coeficientes de regresión. - Las fórmulas para el estadístico F están integradas en los paquetes informáticos. - .hi.pink[Caso de dos restricciones:] Cuando la hipótesis nula conjunta tiene las dos restricciones de que `\(\beta_1 = 0\)` y `\(\beta_2 =0\)`, el estadístico F combina los dos estadísticos `\(t\)`, `\(t_1\)` y `\(t_2\)`, mediante la fórmula: `$$F=\frac{1}{2}\left(\frac{\left.t_{1}^{2}+t_{2}^{2}-2 \hat{\rho}_{t_{1}, t_{2}} t_{1} t_{2}\right)}{1-\hat{\rho}_{t_{1}, t_{2}}^{2}}\right)$$` donde `\(\hat{\rho}_{t_{1}, t_{2}}\)` es un estimador de la correlación entre los dos estadísticos `\(t\)`. --- ## Estadístico F - .hi.pink[Caso general de q restricciones:] Bajo la hipótesis nula, el estadístico F tiene una distribución muestral que, en muestras grandes, está dada por la distribución `\(F_{q,\infty}\)`. Es decir, en muestras grandes, bajo la hipótesis nula el estadístico F se distribuye `\(F_{q,\infty}\)`. --- layout: false class: inverse, middle # Aplicaciones en .mono[R] --- class: inverse, middle # Levantamiento de supuestos --- # Recordemos los supuestos... .pink[Supuesto 1.] Linealidad en parámetros. `$$y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}+u$$` .pink[Supuesto 2.] Muestra aleatoria. `$$\left\{\left(y_{i}, x_{i}\right): i=1, \ldots, n\right\}$$` son variables aleatorias i.i.d. .pink[Supuesto 3.] Exogeneidad estricta. `$$E\left(u \mid x_{1}, \ldots, x_{k}\right)=0$$` .pink[Supuesto 4.] No multicolinealidad. En la muestra, ninguna de las variables independientes es constante y no hay relaciones lineales exactas entre las variables independientes. --- # Recordemos los supuestos... .pink[Supuesto 5.] Homocedasticidad y ausencia de autocorrelación. `\(\operatorname{Var}\left(u \mid x_{1}, \ldots, x_{k}\right)=\sigma^{2}\)` (homocedasticidad) y `\(\operatorname{COV}\left(u_{i}, u_{j} \mid x_{1}, \ldots, x_{k}\right)=0\)` .pink[Supuesto 6.] Normalidad. `$$u\left|x \sim \mathcal{N}\left(0, \sigma^{2}\right)\right|$$` .center[ <img src="images/line.png" width="450">] --- #Omisión de variable relevante .center[  ] --- #Omisión de variable relevante .hi-pink[Sesgo de variable omitida] Si el regresor está correlacionado con una variable que ha sido omitida en el análisis y ésta determina, en parte, la variable dependiente, el estimador MCO presentará sesgo de variable omitida. El sesgo de variable omitida se produce cuando se cumplen dos condiciones: (1) cuando la variable omitida está correlacionada con los regresores incluidos en la regresión y (2) cuando la variable omitida es un factor determinante de la variable dependiente. .purple[Ejemplos:] - Ejemplo #1: Porcentaje de estudiantes de inglés. - Ejemplo #2: La hora del día de la prueba. - Ejemplo #3: Espacio de aparcamiento por alumno. --- #Omisión de variable relevante El sesgo de variable omitida significa que el tercer supuesto de mínimos cuadrados, que `\(E\left(u \mid x_{1}, \ldots, x_{k}\right)=0\)`, no se cumple. ## ¿Por qué se incumple el supuesto 3? Recordemos el término de error `\(u_i\)` en el modelo de regresión lineal con un único regresor representa todos los factores, distintos de `\(X_i\)`, que son determinantes de `\(Y_i\)`. - Si uno de esos otros factores está correlacionado con `\(X_i\)`, esto significa que el término de error (que contiene a este factor) está correlacionado con `\(X_i\)`. En otras palabras, si una variable omitida es un determinante de `\(Y_i\)`, entonces está en el término de error, y si está correlacionada con `\(X_i\)`, entonces el término de error está correlacionado con `\(X_i\)`. --- # Omisión de variable relevante ## ¿Por qué se incumple el supuesto 3? - Debido a que `\(u_i\)` y `\(X_i\)` están correlacionados, la media condicional de `\(u_i\)` dado `\(X_i\)` es distinta de cero. Esta correlación por lo tanto, viola el tercer supuesto de mínimos cuadrados, y la consecuencia es grave: el estimador MCO es sesgado. Este sesgo no desaparece incluso en muestras muy grandes, y el estimador MCO es inconsistente. --- exclude: true <div class="shareagain" style="min-width:300px;margin:1em auto;"> <iframe src="https://taller-5-econometria-1.netlify.app" width="1600" height="900" style="border:2px solid currentColor;" loading="lazy" allowfullscreen></iframe> <script>fitvids('.shareagain', {players: 'iframe'});</script> </div>